EMA(指数平滑移動平均)

| | | Yahoo!ブックマークに登録 | | |

EMA(指数移動平均)はSMA(単純移動平均)の欠点を改善した、高性能な移動平均線で、単純移動平均線よりも素早くトレンドを追うことができる優れたテクニカルチャートです。2009年春頃に大流行し、今や定番となったテクニカルチャートです。なぜそれほどまで大流行したのでしょうか？

EMA(指数移動平均)は今、トレーダーの中で話題のテクニカル分析です。しかし、EMA(指数移動平均)を利用できるFX業者は少なく、EMA(指数移動平均)を利用できるFX事業者を探すのは困難です。そこで、EMA(指数移動平均)対応のおすすめFX事業者をお教えします。

EMA(指数移動平均)のメリット

EMA(指数移動平均)が今、FX界で大きな注目を浴びている理由に、ロンドン在住の元ヘッジファンドマネージャーの某氏(現在プロトレーダー養成会社に在籍)が「FXの超短期トレードで勝つためには、EMAとダウ理論さえあれば十分」と2009年2月の雑誌で発言したことから始まり、今やFXトレーダーの中でEMAは必須のテクニカル分析となっております。

EMA(指数移動平均)は単純移動平均の問題を解決するために開発されました。
単純移動平均の問題は、「常に価格の動きに遅れる」「計算する期間中の価格を等しく平均している」という２点です。大まかなトレンドを把握するには単純移動平均線は優れた分析手法ですが、実際のトレードではあまり使い物になりません。特にFXの様にボラティリティが高く頻繁に値が動く場合ですと、より高速に反応できるチャートが必携です。

移動平均線はあくまでも過去の価格の平均ですから、直近の価格の動きに遅れるのは当然の話ですが、「計算する期間中の価格を等しく平均している」点については、弊害が考えられるのです。

例えば、突発的事象で当日終値が急騰したケースを考えてみてください。価格が大幅に上がるのですから、単純移動平均も上昇します。しかし算出期間内の平均化された比率しか上昇しません。つまり単純移動平均線の動きは鈍いのです。

値動きに遅行するのが移動平均線の性質とは言え、この問題は致命傷になりかねません。 そこで、この問題を改善すべく考え出されたのが、EMA(指数移動平均)なのです 。

しかし、調べてみるとEMAをまともに使用できるFX事業者がとても少ないのです。
短期・中期・長期と複数期間のEMAを同時に表示できるチャートがあればなお良いのですが、なかなか対応していません。EMA(指数移動平均)を4本表示可能で、その他のテクニカル分析やサービスの内容からFXブロードネット
が頭ひとつ抜きん出ている印象です。

EMAを使った売買のサイン

EMAは、直近の値段に比重を置いて算出されているという特徴があります。

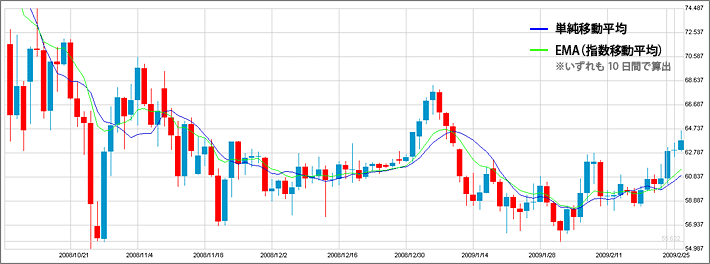
上の図を見ると、EMA(指数移動平均)の方が単純移動平均に比べて価格の動きに敏感に反応していることが分かると思います。
つまり、EMA(指数移動平均)は単純移動平均よりもトレンドを追うのに適した分析方法なのです。

EMAも移動平均線の一種である事には変わりないので、ゴールデンクロスやデッドクロス、グランビルの法則などを当てはめられます。

EMA対応FX事業者

EMA計算式

指数移動平均（EMA：Exponential Moving Average)

単純移動平均よりもトレンドを追うのにすぐれた分析方法、指数移動平均（EMA）があります。
特徴としては直近のデータにより大きな比重をおくので、単純移動平均より早く動きます。
EMAtoday＝EMAyesterday+α×(price-EMAyesterday)
この式で EMAyesterday を展開すると以下のような冪級数となり、各時点の価格 p1, p2 などなどが指数関数的に重み付けされています。
EMA＝P+(1-α)p2+(1-α)2p3+(1-α)3p4+…÷1+(1-α)+(1-α)2+(1-α)3+…
理論上これは総和であるが、1-α が1より小さいため、項はどんどん小さくなってある時点で無視できる大きさになります。また分母は 1/α に近づいていくので(幾何級数のテイラー展開)、分子の無視しない項数を十分に大きくとれば、分母を正確に計算する代わりに1/αを使うことができます。
N日間のEMAと言った場合のNは単にα係数を示すに過ぎず、計算はN日間のデータだけでは済みません。ただし、直近のN日間のデータはEMAにおいて86%の重みを持ち、上の冪級数の式を使って最初のある日のEMAを計算し、その翌日以降は最初のほうで示した式を使います。
99.9% の正確さ（重み付け）を求める場合、
K＝log(0.001×α)÷log(1-α)
となるようKを設定して計算する項目数を決定する。ここで、log(1-α)は N が増えるに従って-2÷(N+1)に近づいていくので、おおよそK=3.45×(N+1)とすればほぼ99.9%の正確さとなります。
なお、α=2÷(N+1)ではなくα=1÷NとするEMAもあります。